A guide for the Perplexed- Convexity Maven

Harley Bassman writes “Convexity is always lurking at the scene of the crime ”
Wall Street loves to make convexity sound complex (I suppose it’s so they can charge higher fees ?). We speak Greek (calling it “gamma”), employ physics as a metaphor (analogizing to it “acceleration”), and use mathematical definitions (since it is the second derivative of the asset’s price change).
Pish, posh. An investment is convex if the payoff is unbalanced for equally opposite outcomes. So if there’s the potential to earn a profit of two on a bet versus a maximum loss of one, the bet is positively convex. If you can lose three versus making two, it is negatively convex. That’s it. The rocket scientists are called upon to help (fairly) price the cost (value) of such possible outcomes. This is why the expansion of derivative trading in the 1990’s resulted in a hiring spree of physics PhD’s.
Investors have a conflicted relationship with convexity. It has been observed that the unpleasantness of losing one dollar is greater than the joy of making a similar sum; a social economist would say that people are not risk neutral. Yet incongruously, investment managers display a bias to be short optionality (convexity); a payoff profile where the losses can be greater than the gains.

The reason is simple: Convexity (option) sellers are paid up front, either via a coupon or cash (the option premium). In a nutshell, greed outweighs fear.
For simplicity, let’s assume that US Treasuries (UST) have no convexity, so their yield is just the pure risk-free interest rate received to maturity. As such, we can model a non-callable corporate bond as a UST plus some extra yield for the risk the company cannot ultimately return your money. This will sort of look like being long a UST and short a put on the company’s stock, but more accurately short a credit default option on the company.
A greater risk of default translates into a more expensive option and thus, a higher yield on such bonds. Presently, a bond issued by Apple yields about 42bps more than a similar maturity UST, while a bond backed by Tesla offers an extra yield of 406bps. Investment professionals will ponder which has a better ‘risk-adjusted return’; but there no is doubt that buyers of Tesla bonds will receive an extra 364bps as long as Elon’s company can make the coupon payments.
Among the many under-appreciated consequences of the Fed’s Zero Interest Rate Policy (ZIRP) was how liability managers (pension / insurance) might overweight convexity risk in their effort to reach their return targets. This demand explains the massive growth in the -labrador bar- BBB-rated market relative to the -gingerline bar- BB-rated market

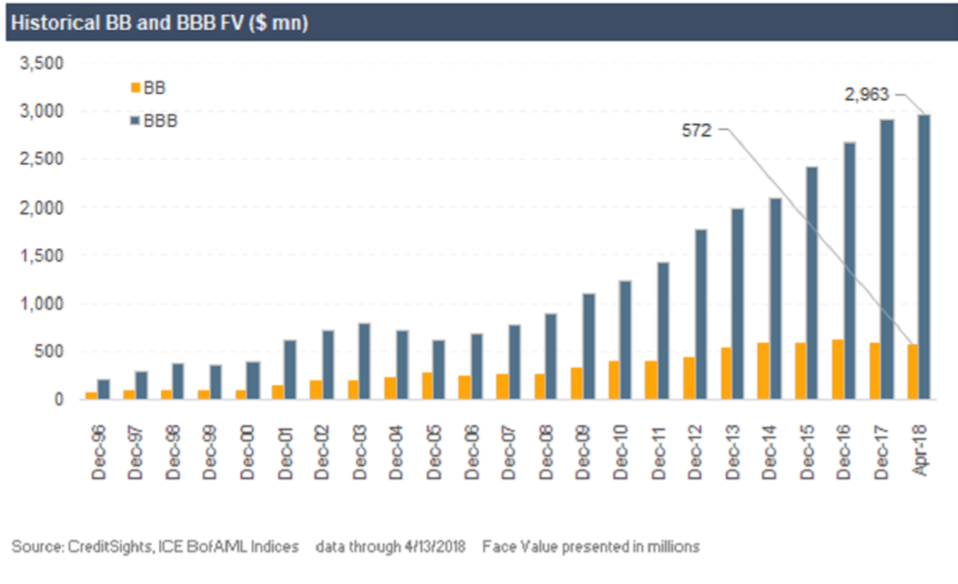
An option is most convex when it is at-the-money; a location where it also has the greatest time value (yield). BBB-rated bonds reside at the credit inflection point – a notch lower and they become “junk” that may need to be quickly liquidated by investment-grade portfolios.

Harley concludes …….
I am loath to use the word “always”, but over the course of my professional career, there always seems to be a concentration of short convexity at the core of extreme market turbulence. Convexity is the measure of unbalanced risk so, almost by definition, a negatively convex portfolio will be unstable. Markets become disturbed when the instability of convexity becomes greater than the market’s liquidity.
Convexity is not the match, but rather the accelerant.